Математика

Зміст:

1. Основні тригонометричні тотожності
2. Тригонометричні перетворення (симетрія та зсув)
3. Обернені тригонометричні функції
4. Таблиця тригонометричних функцій (0°–360°)
5. Похідні основних функцій
6. Первісні деяких функцій
7. Корені тригонометричних функцій
8. “Великі формули” (~50)

Основні тригонометричні тотожності

• sin² α + cos² α = 1
• tg α × ctg α = 1
• tg² α + 1 = 1 / cos² α
• ctg² α + 1 = 1 / sin² α

Тригонометричні перетворення (симетрія та зсув)

α = 0	α = π/2	α = π
sin(-α) = -sin α	sin(π/2 - α) = cos α	sin(π-α) = sin α
cos(-α) = cos α	cos(π/2 - α) = sin α	cos(π-α) = -cos α
tg(-α) = -tg α	tg(π/2 - α) = ctg α	tg(π-α) = -tg α
ctg(-α) = -ctg α	ctg(π/2 - α) = tg α	ctg(π-α) = -ctg α

+ π/2	+ π	+ 2π
sin(α + π/2) = cos α	sin(α+π) = -sin α	sin(α+2π) = sin α
cos(α + π/2) = -sin α	cos(α+π) = -cos α	cos(α+2π) = cos α
tg(α + π/2) = -ctg α	tg(α+π) = tg α	tg(α+2π) = tg α
ctg(α + π/2) = -tg α	ctg(α+π) = ctg α	ctg(α+2π) = ctg α

Обернені тригонометричні функції

f(arcf x) = x	arcf(f x) = x
sin(arcsin x) = x	arcsin(sin x) = x
cos(arccos x) = x	arccos(cos x) = x
tg(arctg x) = x	arctg(tg x) = x
ctg(arcctg x) = x	arcctg(ctg x) = x

Таблиця тригонометричних функцій (0°–360°)

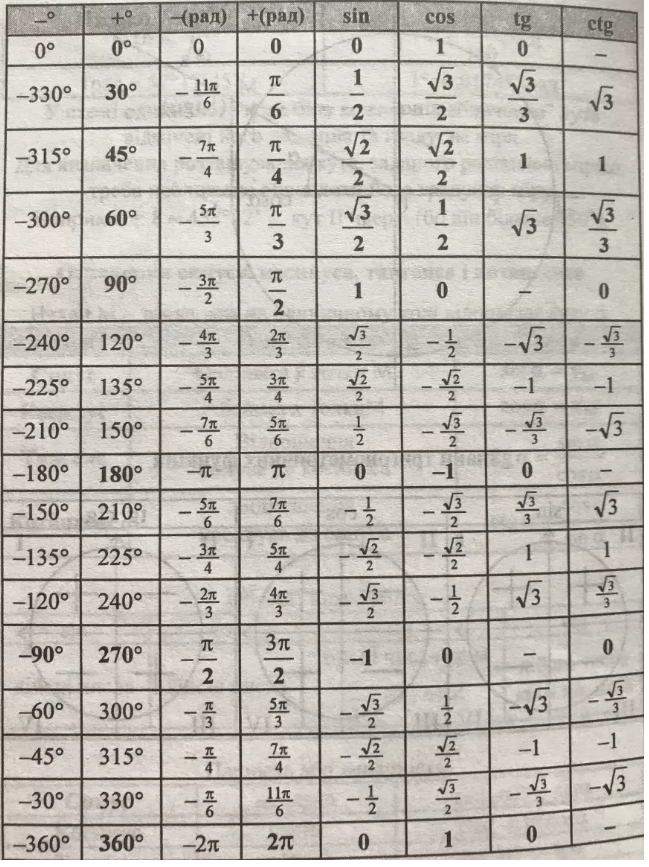
Похідні основних функцій

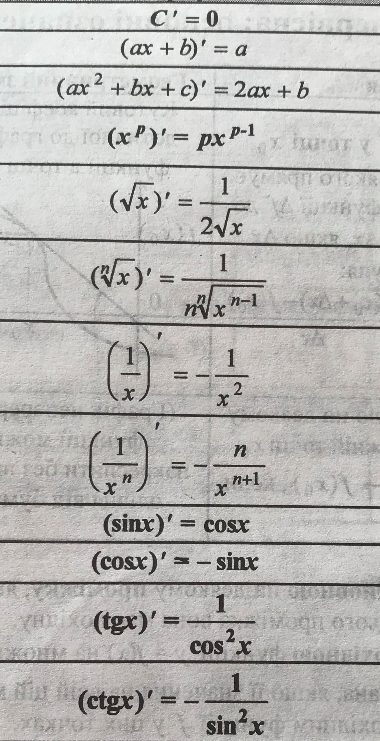
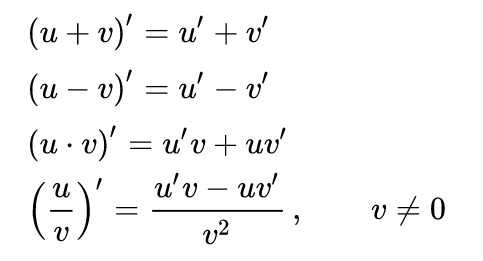
Первісні деяких функцій

Корені тригонометричних функцій

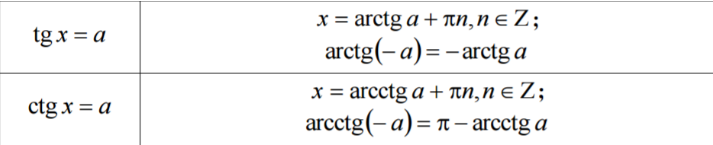
“Великі формули” (~50)